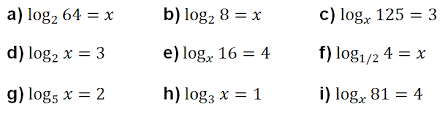OPERACIONES CON LOS N. NATURALES

El significado de los números es el de contar. Tal y como las letras se usan para representar sonidos y los colores se usan para representar imágenes, los números se usan para representar cantidades. Hay diez números naturales que son los que conocemos del 1 al 9, y todos los demás son compuestos de estos números.

¿Y qué hay del cero (0)? Pues el cero siempre ha sido cuestión de debate, porque algunos dicen que es un número para representar la nada, mientras que otros dicen que al no representar una cantidad concreta no debería ser considerado como un número o cantidad. El cero empieza a tener relevancia cuando va a la izquierda de otro número, como en el caso del '10', que viene después del nueve.

La secuencia va de derecha a izquierda.
A partir del 10 todos los números comienzan a llevar dos cifras.
Un número con dos cifras estará compuesto de un solo número al lado derecho del otro, igual que con tres cifras. Jamás pueden haber dos números en el mismo puesto que otro al momento de escribirse.

Operaciones algebraicas con supresiones de signos de agrupación

Las sumas algebraicas muchas veces resultan de combinar y agrupar los diferentes términos usando diferentes símbolos como paréntesis ( ), corchetes { } y llaves [ ]. Cuando se plantean dichas sumas, se establece un orden de escritura de adentro hacia afuera: primero paréntesis, seguido de corchetes y más externamente, las llaves: . En estos casos se aplica sin falta, la ley de los signos en las cuatro operaciones matemáticas básicas ya mencionadas. Mediante varios ejemplos, amigos estudiantes veremos lo sencillo que es su resolución

[ 4 + (-12+15) ] =

[ 4 + (3) ] =

Para resolver esta suma algebraica, se puede escoger hacer los cálculos de adentro hacia afuera: primero paréntesis, seguido de los corchetes. De lo contrario, de afuera hacia adentro: primero corchete y de último los paréntesis. El resultado será el mismo, pero debes escoger solo una forma, manteniendo el orden de tus cuentas para que no pierdas la secuencia. Vamos a hacerlo de las dos formas para que veas lo fácil que es

(Al resolver el paréntesis, se observa una suma de diferentes signos)

Ejemplo 2

b. {2 +3.[6+3.(7+2)+1]} = De adentro hacia afuera

Resolvemos lo que está dentro del paréntesis y el valor externo a él aplicando propiedad distributiva, desapareciendo los paréntesis, lo demás queda igual, no lo toquen:

{2 +3.[6+3.(9)+1]}

{2 +3.[6+27+1]}

{2 +3.[34]}

{2 +102 }

104

MULTIPLICACIONES POR UNA Y DOS CIFRAS

• Para multiplicar un número por una sola cifra, se multiplica se multiplica el número por las unidades, luego, por las decenas, por las centenas y así sucesivamente. Si es necesario se agrupa. • Para multiplicar un número por dos cifras, se multiplica primero por las unidades y luego por las decenas como si fuera por una cifra; el producto de la segunda cifra se ubica a partir de las decenas del primer producto. Luego, se suman los dos productos para dar el producto final.

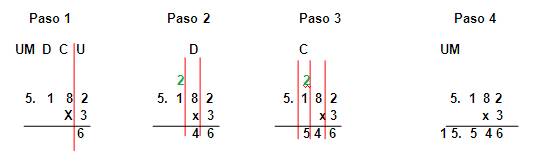
Multiplicación Por Una Cifra

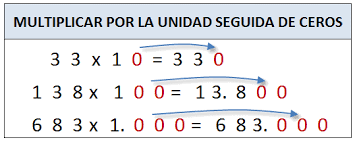
• MULTIPLICACIONES ABREVIADAS MULTIPLICACIÓN POR 10, 100, 1 000, 10.000 ......

Ejemplo: 15 x 100 = Se escribe el 15 y se le agregan 2 ceros del 100: = 1500 Luego

DIVISION POR UNA O VARIAS CIFRAS:

La división es la operación inversa a la multiplicación.

Consiste en averiguar cuántas veces el divisor está contenido en el dividendo.

D : d = c

El dividendo (D) es el número que ha de dividirse por otro.

El divisor (d) es el número entre el que ha de dividirse otro.

El cociente (c) es el resultado de la división.

Para la notación de la división se emplea entre el dividendo y el divisor los signos:

Se representa mediante los signos: dos puntos :, barra diagonal / u óbelo ÷

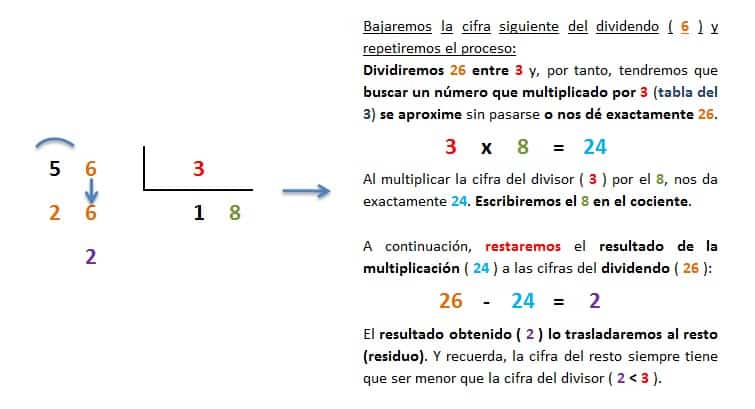
División Por Dos Cifras

EJERCICIOS PROPUESTOS

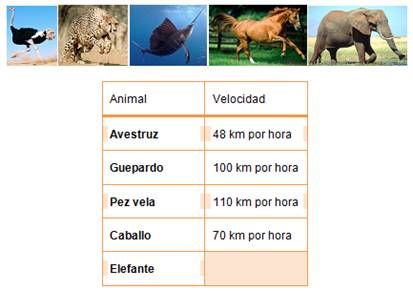
1 Si el pez vela es el más rápido, ¿Cuál es la diferencia con el más lento?

Sumando la velocidad del guepardo y el caballo, ¿Cuál es la diferencia con el pez vela?

¿ Cuál es resultado del producto de la velocidad de la avestruz y el caballo?

¿ Cuál es resultado del producto de la avestruz y el geopardo?

2.Busca el término desconocido e indica su nombre en las siguientes operaciones:

a 327 + ________ =1280

b _____ - 4121= 621

c 321* ________ = 32100000

d 28035 / ____ = 623

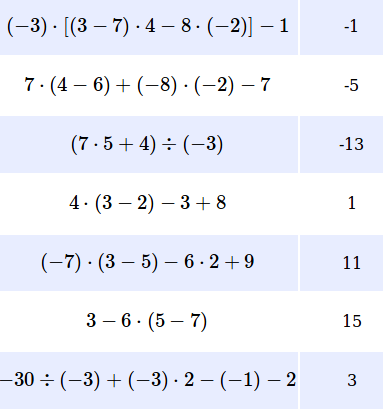
3. Una con una flecha los respectivos resultados.

POTENCIA, RADICACIÓN Y LOGARITMACIÓN

EJE TEMATICO: LA POTENCIACIÒN LOGRO Relaciona operaciones donde establezca la diferencia y calculo entre la potenciación, radicación y logaritmación.

En esta guía se pretende socializar los conocimientos matemáticos relacionados con la potenciación y la radicación. .Es muy útil propiciar en el aula la capacidad de estimar y comparar números utilizando diversas estrategias: bloques base diez, recta numérica, calculadora, ábaco..., que permiten una elaboración mental más profunda de los números. Iniciarás con la fase de concienciación y explicación del tema, luego realizarás el planteamiento de actividades teniendo en cuenta las competencias interpretativa, argumentativa y propositiva.

POTENCIACIÓN

Potenciación La potenciación es una multiplicación abreviada de factores iguales.

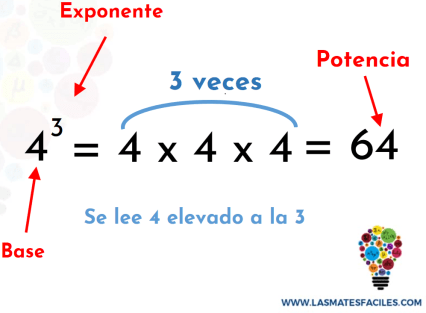
Ejemplo 1 Exprese como potencia los siguientes productos

a) 3 × 3

b) 5 × 5

c) 7 × 7 × 7 × 7 × 7 × 7

Solución: a) 3 × 3 = 3² b) 5 × 5 = 5² c) 7 × 7 × 7 × 7 × 7 × 7 = 7⁶

Ejemplo 2

Identifique los términos de las siguientes potencias

a) 4⁵ = 1.024 4⁵ = 1.024 Base = 4 Exponente = 5 Potencia = 1.024

b) 3⁴ = 81 3⁴ = 81 Base = 3 Exponente = 4 Potencia = 81

c) 10³ = 1.000 10³ = 1.000 Base = 10 Exponente = 3 Potencia = 1.000

RADICACIÓN

La radicación es la operación que consiste en buscar un número que multiplicado por sí mismo una cantidad de veces resulte otro número determinado. Calcular la raíz enésima de un número entero es encontrar otro número que elevado a un exponente n sea igual al primero

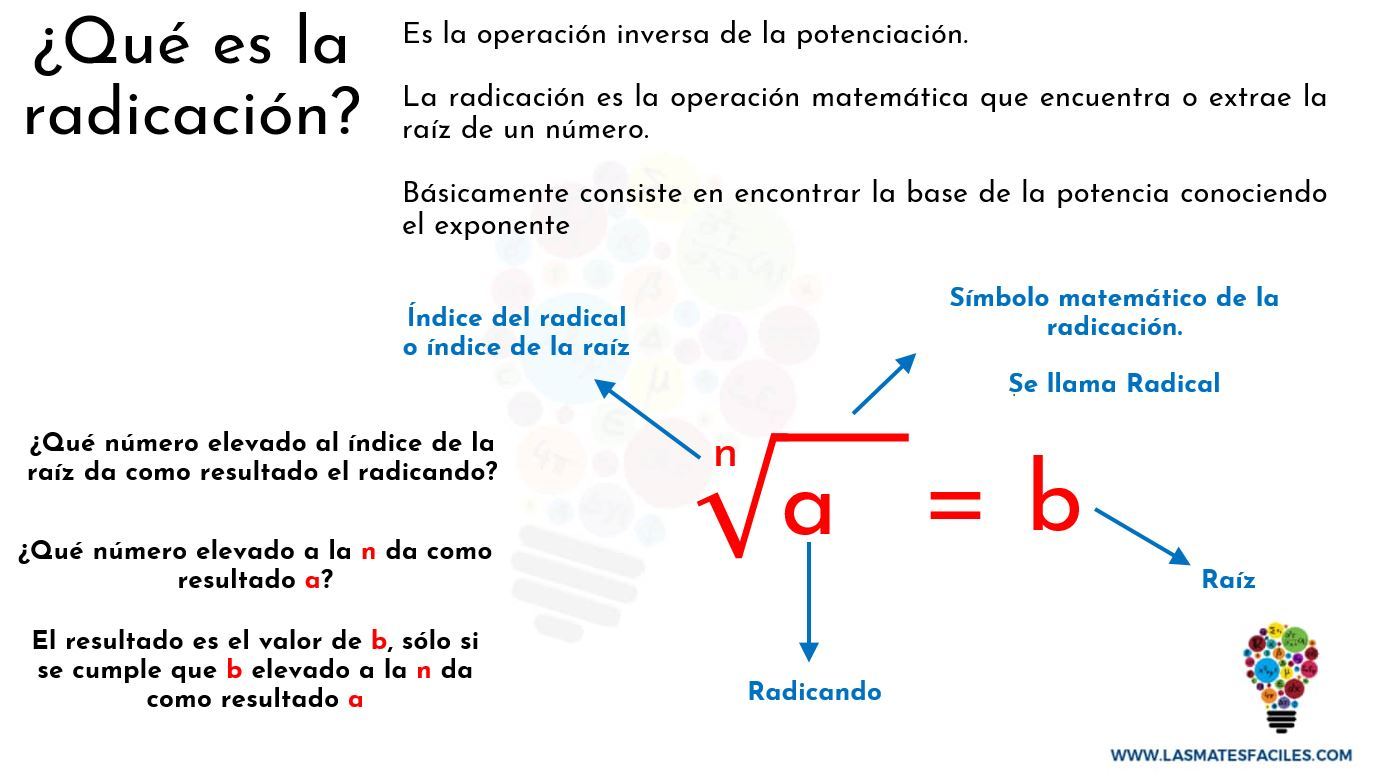
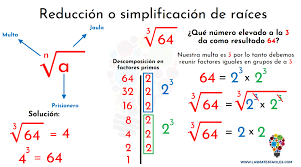
Por ejemplo: Supongamos que nos encontramos con un radical que muestra la raíz cubica de 64. Tendremos el radicando (64) y el índice o exponente (6, ya que es una raíz sexta). A través de la radicación, llegamos a la raíz: 3. Esto quiere decir que 2 elevado a la seis (2 x 2 x 2) x (2 x 2x 2) es igual a 64. Vemos que multiplicando (2 x 2 x 2)x (2 x 2x 2) (2 elevado a la tres) llegamos a la raíz cubica de 64.

Raíz de un producto La raíz de un producto es igual al producto de las raíces de los factores:

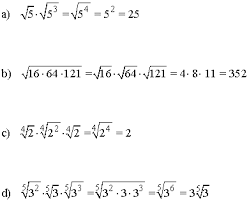
Raíz de un cociente La raíz de una fracción es igual al cociente de la raíz del numerador entre la raíz del denominador:

EJERCICIOS PROPUESTOS

1. Identifique los términos de las siguientes potencias

a) 9¹

b) 6³

c) 1²

d) 4⁴

2. Resuelva las siguientes potencias

a) 4⁵

b) 3⁴

c) 10³

(2³ × 3⁴ × 5²)³

3¹² × 7⁴/ 7² × 3⁹

3 × 5⁶ × 11⁵ / 5⁴ × 11⁰ × (2) ²

4, Don Víctor tiene almacenadas 7 cajas. En cada caja tiene 7 bolsas y en cada bolsa tiene 7 chocolates. ¿Cuántos chocolates tiene almacenados don Víctor? Utilice el espacio para hacer el proceso.

5. La Hidra de Lerna es un personaje mitológico que aparece en algunas historias, como la de las 12 pruebas de Hércules. La Hidra era un monstruo con 1 cabeza, pero por cada cabeza que se le cortara, le nacían 2 cabezas en su lugar. Si un héroe intentaba vencerla cortándole todas sus cabezas cada día, ¿Cuántas cabezas tendría la Hidra el tercer día? Utilice el espacio para hacer el proceso?

LOGARITMOS EN LOS NATURALES

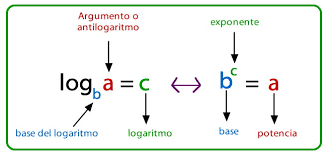
De la definición de logaritmo podemos decir que:

No existe el logaritmo con base negativa.

No existe el logaritmo de un número negativo.
No existe el logaritmo de cero.